2023太原站wtt常规挑战赛比赛时间是从11月7日开始吗?
2023-10-30
更新时间:2023-09-10 16:08:17作者:无忧百科


新智元报道
编辑:桃子 润
【新智元导读】英伟达首席科学家揭秘英伟达GPU能如此成功的4个主要原因,4个关键数据带来持续的行业竞争力。
如今的英伟达,稳坐GPU霸主王座。
ChatGPT诞生后,带来生成式AI大爆发,彻底掀起了全球的算力争夺战。
前段时间,一篇文章揭露,全球对H100总需求量超43万张,而且这样的趋势至少持续到2024年底。

过去的10年里,英伟达成功地将自家芯片在AI任务上的性能提升了千倍。
对于一个刚刚迈入万亿美元的公司来说,是如何取得成功的?
近日,英伟达首席科学家Bill Dally在硅谷举行的IEEE 2023年热门芯片研讨会上,发表了关于高性能微处理器的主题演讲。
在他演讲PPT中的一页,总结了英伟达迄今为止取得成功的4个要素。
摩尔定律在英伟达的「神奇魔法」中只占很小的一部分,而全新「数字表示」占据很大一部分。
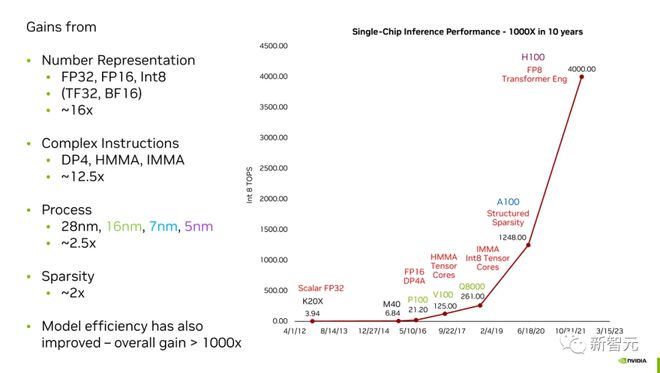
英伟达如何在10年内将其GPU在AI任务上的性能提高了千倍
把以上所有这些加在一起,你就会得到「黄氏定律」(Huang's Law)。
黄教主曾表示,「由于图形处理器的出现,摩尔定律已经站不住脚了,代之以一个新的超强定律。」

数字表示:16倍提升
Dally表示,总的来说,我们最大的收获是来自更好的「数字表示」。
这些数字,代表着神经网络的「关键参数」。
其中一个参数是权重,模型中神经元与神经元之间的连接强度。
另一个是激活度,神经元的加权输入之和乘以多少才能决定它是否激活,从而将信息传播到下一层。
在P100之前,英伟达GPU使用单精度浮点数来表示这些权重。
根据IEEE 754标准定义,这些数字长度为32位,其中23位表示分数,8位基本上是分数的指数,还有1位表示数字的符号。
但机器学习研究人员很快发现,在许多计算中,可以使用不太精确的数字,而神经网络仍然会给出同样精确的答案。
这样做的明显优势是,如果机器学习的关键计算——乘法和累加——需要处理更少的比特,可以使逻辑变得更快、更小、更高效。
因此,在P100中,英伟达使用了半精度FP16。
谷歌甚至提出了自己的版本,称作bfloat16。
两者的区别在于分数位和指数位的相对数量:分数位提供精度,指数位提供范围。Bfloat16的范围位数与FP32相同,因此在两种格式之间来回切换更容易。

回到现在,英伟达领先的图形处理器H100,可以使用8位数完成大规模Transformer神经网络的某些任务,如ChatGPT和其他大型语言模型。
然而,英伟达却发现这不是一个万能的解决方案。
例如,英伟达的Hopper图形处理器架构实际上使用两种不同的FP8格式进行计算,一种精度稍高,另一种范围稍大。英伟达的特殊优势在于知道何时使用哪种格式。

Dally和他的团队有各种各样有趣的想法,可以从更少的比特中榨取更多的人工智能性能。显然,浮点系统显然并不理想。
一个主要问题是,无论数字有多大或多小,浮点精度都非常一致。
但是神经网络的参数不使用大数,而是主要集聚在0附近。因此,英伟达的R&D重点是寻找有效的方法来表示数字,以便它们在0附近更准确。
复杂指令:12.5倍
「提取和解码指令的开销远远超过执行简单算术操作的开销,」 Dally说道。
他以一个乘法指令为例,执行这个指令的固定开销达到了执行数学运算本身所需的1.5焦耳的20倍。通过将GPU设计为在单个指令中执行大规模计算,而不是一系列的多个指令,英伟达有效地降低了单个计算的开销,取得了巨大的收益。
Dally表示,虽然仍然存在一些开销,但在复杂指令的情况下,这些开销会分摊到更多的数学运算中。例如,复杂指令整数矩阵乘积累加(IMMA)的开销仅占数学计算能量成本的16%。
摩尔定律:2.5倍
保持摩尔定律的有效性需要数十亿美元的投资、非常复杂的工程上的设计,甚至还会带来国际关系的不稳定。但这些投入都不是造成英伟达GPU的成功的主要原因。
英伟达一直在使用全球最先进的制造技术来生产GPU——H100采用台积电的的N5(5纳米)工艺制造。这家芯片工厂直到2022年底才开始建设它的其下一代N3工艺。在建好之前,N5就是业内最顶尖的制造工艺。
稀疏性:2倍
将这些网络变得「稀疏」以减少计算负荷是一项棘手的工作。
但是在A100,H100的前身中,英伟达引入了他们的新技术:「结构化稀疏性」。这种硬件设计可以强制实现每四个可能的剪枝事件中的两次,从而带来了一种新的更小的矩阵计算。
Dally表示:「我们在稀疏性方面的工作尚未结束。我们需要再对激活函数进行加工,并且权重中也可以有更大的稀疏性。」
参考资料:
https://spectrum.ieee.org/nvidia-gpu

